Eigenfactor與Article Influence介紹─JCR期刊評鑑指標(2)

Posted on by

在「JCR中各項指標的意義為何？」一文中，介紹過以Web of Science資料庫為基礎所建置的期刊評鑑資料庫JCR之各項指標意義，本文將針對其中的 Eigenfactor 與 Article Influence 作較詳細的介紹。

Eigenfactor (特徵係數，或稱特徵因素) 由美國華盛頓大學 Carl T .Bergstrom 教授所領導的研究小組提出。其概念與本站先前介紹的SJR非常類似(請參考「SJR─SCOPUS期刊評鑑指標(1)」一文)，較傳統Impact Factor的主要突破在於“將期刊間的引用給予不同的權重”，意即被聲望高的期刊所引用，對聲望的提升應較被一般期刊引用來得顯著，反之亦然。Eigenfactor以JCR為計算基礎，計算之時間區間為5年，意即某期刊2007年的Eigenfactor值，是透過計算其前5年(2002~2006年)間發表的文章，於2007年被引用的次數。Eigenfactor完全排除自我引用，亦即相同期刊內不同文章的互相引用，將不計入該期刊的被引次數中。這三點是與SJR明顯不同的前提(SJR以SCOPUS為計算基礎，採計的時間區間為3年，且允許33%的自我引用上限)。

Eigenfactor核心概念與Google的PageRank演算法的“「隨機瀏覽」(random surfer)”相同(請參考延伸閱讀「PageRank簡介」一文)，從隨機挑選期刊開始，可選擇follow期刊文章引用的任一參考文獻閱讀下一本期刊，或無視參考文獻，隨機跳到其他任一本期刊，如此反覆不斷進行隨機閱讀，而Eigenfactor就是以計算在這個過程中各期刊被閱讀到的機率為主要概念的指標。

 

Eigenfactor計算可分為以下三大步驟，以下將循序介紹：

  1. 首先透過期刊間的引用網絡建立引用矩陣。
  2. 以「隨機瀏覽」概念計算出各期刊被閱讀到的機率，稱之為影響向量(Influence Vector)。
  3. 最後將Influence Vector代回原先建立的矩陣算出期刊的最終Eigenfactor。

 

  1. 建立引用矩陣

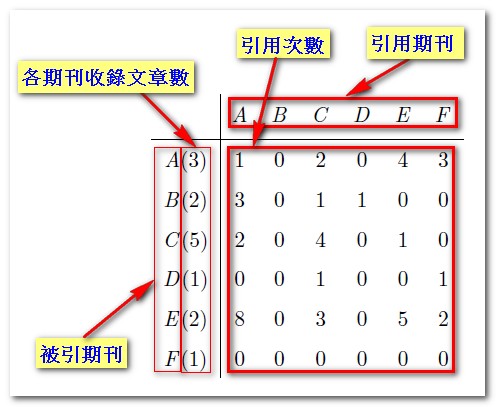
首先將各期刊間的引用關係、與期刊收錄文章建立如下的矩陣：

 

(橫軸為引用期刊，縱軸為被引期刊，例如A期刊引用A期刊1次、B期刊3次、C期刊2次、D期刊0次、E期刊8次、F期刊0次，C期刊引用A期刊2次、E期刊3次，以此類推；括弧內為各期刊文章收錄數，例如B期刊2篇、C期刊5篇，以此類推)

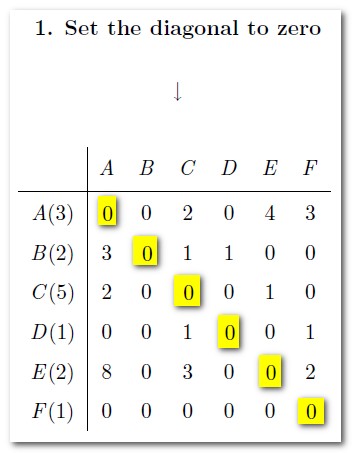
因為Eigenfactor完全排除自引，因此將對角線的自引數全部歸零：

 

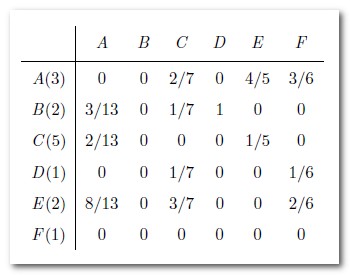
為計算從引用期刊到被引期刊的機率，將原始被引數/引用期刊的總引用數，得到H矩陣如下：

(A期刊總引用13次，因此將B、C、E期刊被A引用的次數都除以13，以此類推)

–

2. 計算Influence Vector(簡稱IV)

影響向量(Influence Vector)以前述的「隨機瀏覽」概念，計算各期刊被閱讀到的機率。首先將「隨機瀏覽」過程中，follow參考文獻挑選下一本閱讀期刊的機率訂為85%，不follow參考文獻而隨機跳讀任一期刊的機率訂為15%。以下說明這兩部分應如何計算：

  • Follow參考文獻(85%)：按前述H矩陣的引用比例計算。例如閱讀到A期刊，追蹤其參考文獻，就有3/13的機率會閱讀到B期刊、2/13的機率到C期刊、8/13的機率到E期刊，以此類推。這個機率再乘以A期刊被看到的機率，就是B、C、E期刊被看到的機率。
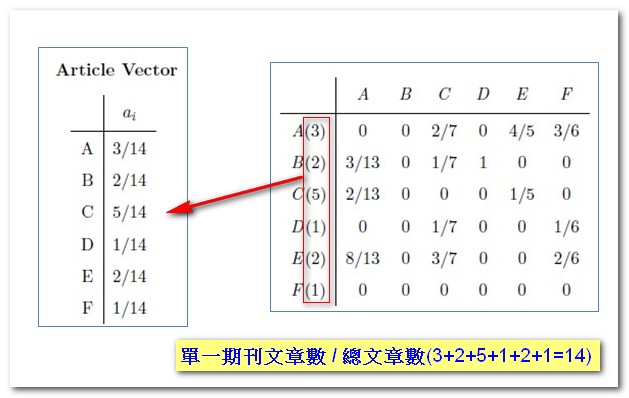
  • 不follow參考文獻(15%)：按各期刊文章數佔所有期刊總文章數的比例，推估各期刊機率。以此例而言，6本期刊共有14篇文章，則A期刊被看到的機率為3/14、B期刊為2/14，以此類推。此比例稱為Article Vector，如下：

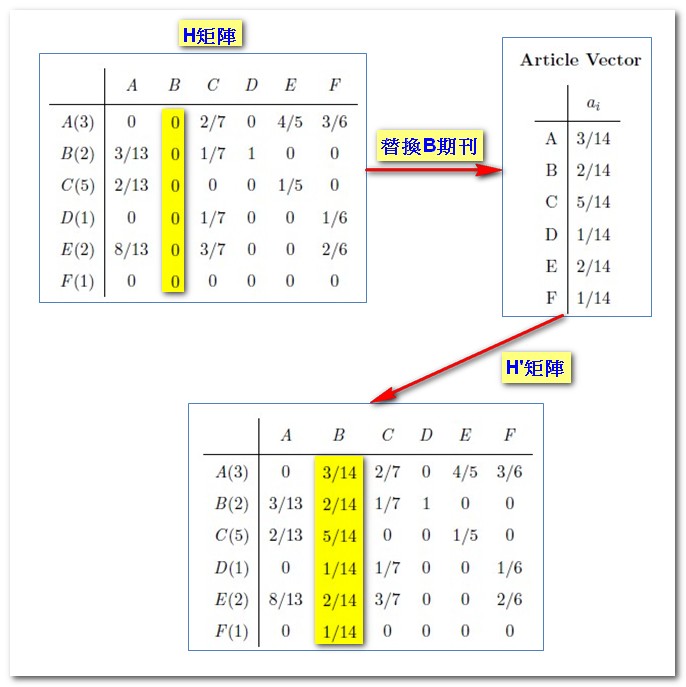
其中需特別注意在Follow參考文獻的部分，當遇到沒有參考文獻的期刊(如B期刊)時，因無法追蹤其引文，因此也將會是隨機跳讀任一期刊的狀況，就以前述的Article Vector替換，形成H’矩陣如下：

 

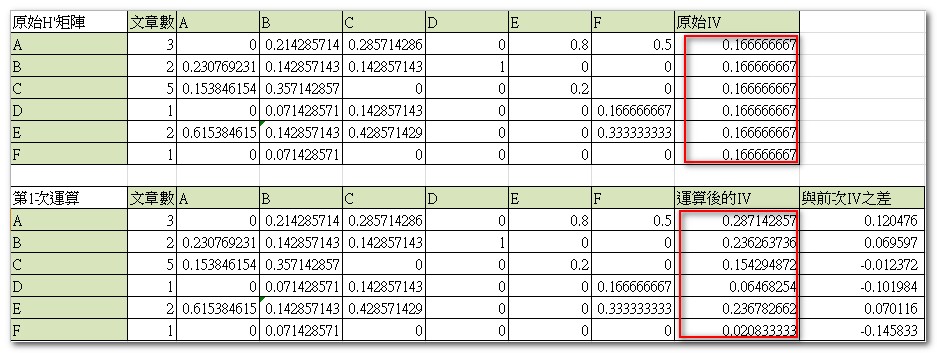
Influence Vector(簡稱IV)即是透過以上兩部分的運算結果加總，並將加總結果重複代回H’矩陣運算，直至結果收斂為趨近值而得。初始時各期刊被看到的機率均等，因此各期刊IV均為1/6，以A期刊為例，其兩部分的計算如下：

  • Follow參考文獻(85%)：A被C、E、F期刊引用，將獲得引用期刊的Influence Vector*佔該引用期刊之引用比例的機率；另外B期刊因無引用，如前述將按Article Vector分配引用比例，因此在這部分A期刊將獲得：(B的IV*A的Article Vector)+( C的IV*A佔C的引用比例)+( E的IV*A佔E的引用比例)+ (F的IV*A佔F的引用比例)=[(1/6)*(3/14)]+ [(1/6)*(2/7)]+ [(1/6)*(4/5)]+ [(1/6)*(3/6)]。

 

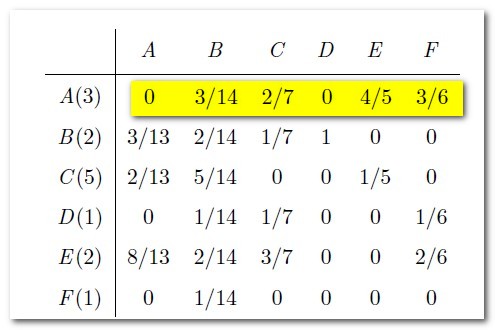
  • 不follow參考文獻(15%)：如前述，按該期刊的Article Vector分配，因此A獲得3/14。

將兩部分加總，A期刊在第一次運算所獲得的IV為：0.85*{[(1/6)*(3/14)]+ [(1/6)*(2/7)]+ [(1/6)*(4/5)]+ [(1/6)*(3/6)]}+0.15*(3/14)=0.2871。各期刊均以此類推，第一次運算的IV結果如下：

 

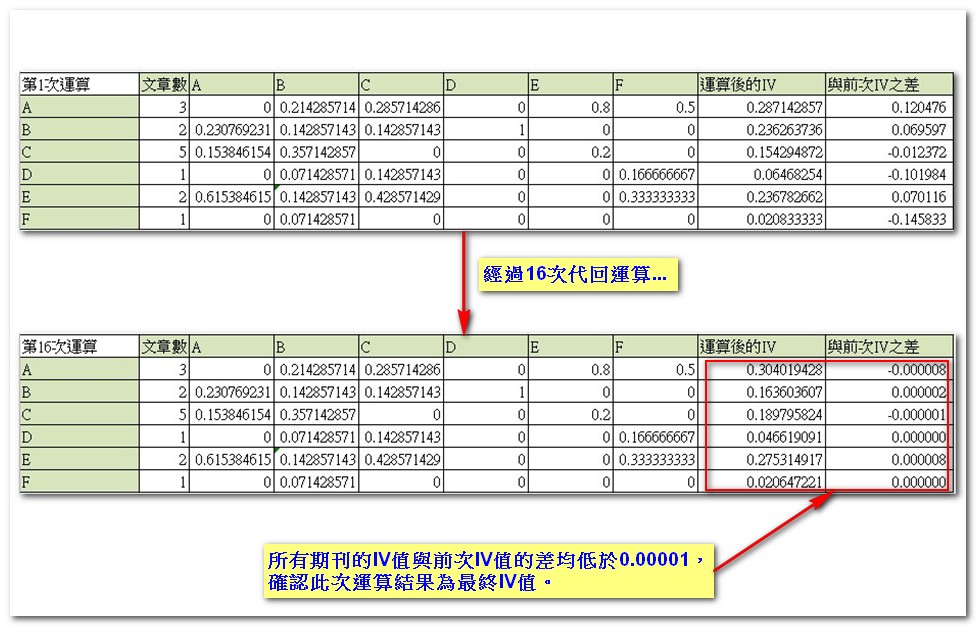
運算後的IV，將代回H’矩陣重複運算，直到結果收斂至趨近值。這裡的趨近定義為運算後的IV與前一次IV相差在0.00001以內，也就是當所有期刊的IV值均達到此標準，即可確立最終的IV值。以此例而言，在經過16次代回運算之後，將可得到最終的IV值(詳細請參考EF與AI運算歷程數據)：

 

透過以上的運算，我們可以體會到Influence Vector如何將引用權重的概念落實到實際的演算：

  • 當一個期刊被引用得越多，其越容易累積來自引用期刊的IV值，而使自身的IV值提高。
  • 被IV值越高的期刊引用，所獲得的IV值也將越高。
  • 向外引用較少的期刊，其所能貢獻給個別引用期刊的IV值將越高。

–

3. 計算Eigenfactor

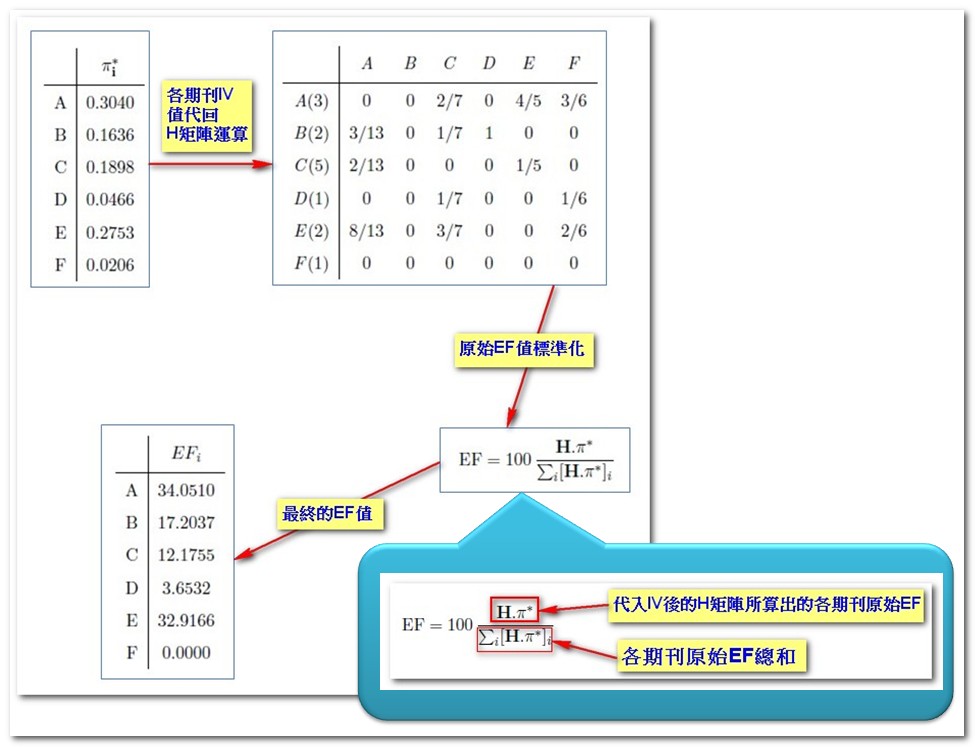
最後一部分就是將上一階段計算出的Influence Vector代回原本的H矩陣，計算出Eigenfactor(簡稱EF)。因為原始的H矩陣並沒有將無參考文獻的期刊替換為Article Vector，因此計算出的EF將部分流失而總和不為1。為使EF值標準化，會將各期刊的原始EF值除以所有期刊EF值的總和，並將結果乘以100以呈現百分比數值，所得結果即為最終的Eigenfactor值，流程如下：

 

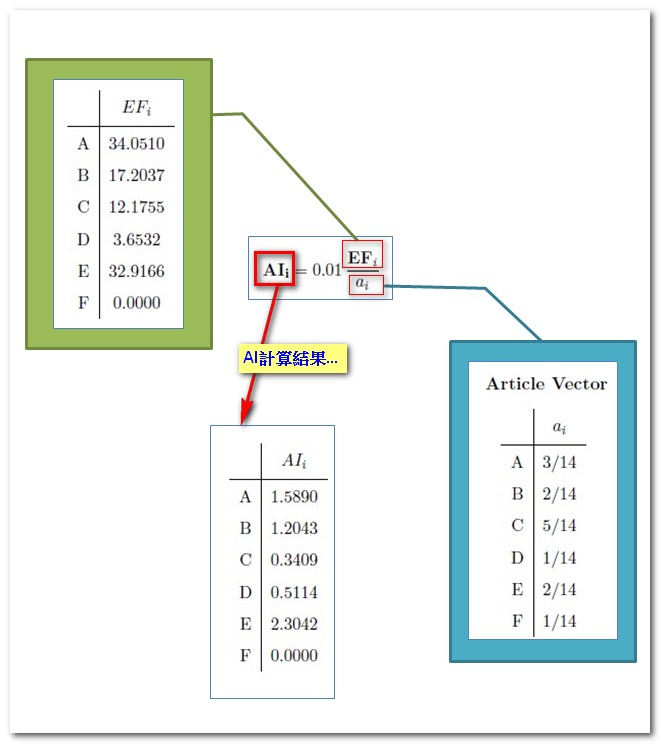
求得Eigenfactor後，另一項Article Influence指標就呼之欲出了！Article Influence在計算期刊中單篇文章的影響力，將期刊原始的EF值，除以該期刊的Article Vector，也就是除以該期刊文章量於整個母群所有文章量的比例。將此運算後的數據乘以0.01，即為Article Influence。

–

以上為期刊評鑑指標Eigenfactor與Article Influence的運算簡介，其發想自PageRank的隨機瀏覽，突破傳統Impact Factor單純計算引用次數而無法反映個別引用“價值”的缺陷，也提供了我們在評價學術期刊時的另一種參考指標。

參考資料：

By 張育銘

 

【期刊評鑑系列相關推薦】

【輔助閱讀】